Étienne Simon's homepage: ~/projects/LIP6 2014

Reasoning on representations learnt by neural networks

Problem

Capitals' points are on the left, countries' points on the right, the vector between a country and its capital is nearly constant. — Figure 1: 2D PCA projection of Skip-gram vectors from [1]. The relation "capital of" appears as a translation while learning embeddings for words.

Given a set of entities E, a set of relations R and a training set composed of triplets (h, r, t) with h, t ∈ E and r ∈ R (e.g. (Rome, capital of, Italy)); learn a representation for E and R in order to predict unseen triplets.

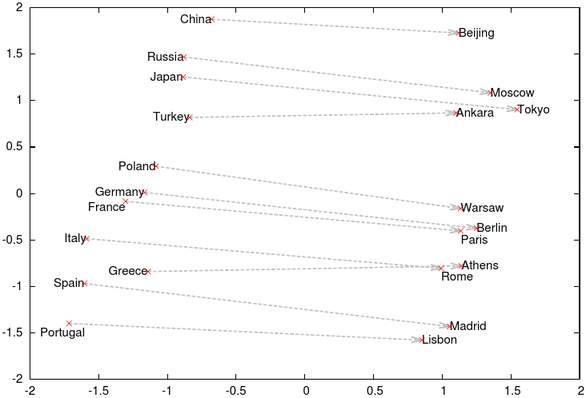
In [1], Tomas Mikolov exhibits figure 1 which nicely shows what Antoine Bordes exploits in [2] : while learning embeddings for words, relations between them appear as translations.

In [2], Antoine Bordes proposes the following model : entities and relations are represented as d-dimensional vectors (with d≈50). If (h, r, t) is true then h+r≈t. Each triplet (h, r, t) is given a score sim(h+r, t) where sim is a similarity function (usually L1 norm or cosine). In order to learn the matrices E and R, a contrastive objective is used, for each valid triplet (h, r, t), two corrupted entities are picked h', t' ∈ E, the left score of the triplet is defined as: $\max(0, γ + sim(h+r, t) - sim(h'+r, t))$ Were, γ is the contrastive margin. Similarly, the right score is defined by replacing the third member of the triplet instead of the first, the final objective is to minimize is the sum of the left and right score.

A nice example of dataset is Freebase, it shows that a solution to this problem could be used as an inference engine to solve general question/answer.

Solutions

Reimplementation : Link to the repository.

Other transformations

The first tentative was to replace the translation x+r by some other transformation, here is a list:

Name	Equation	2D Illustration	Similarity	FB15k
				Micro		Macro
				Mean	Top10	Mean	Top10
Translation	x+r		L1	233.61	36.74	361.27	32.98
			L2	309.67	29.85	257.22	46.79
			Cosine	690.36	14.37	690.95	19.64
Point reflection	2⁢r-x		L1	298.27	31.91	626.19	32.00
			L2	419.04	23.75	582.00	39.52
			Cosine	1564.66	16.43	2244.51	21.48
Reflection	$x - 2 (x·r)/(r·r) r$		L1	249.16	29.27	269.25	29.15
			L2	378.53	21.45	456.99	27.92
			Cosine	401.18	20.24	383.67	25.43
Offsetted reflection	$x - 2 (x·r₀ - r₁)/(r₀·r₀) r₀$		L1	251.96	33.26	275.61	29.51
			L2	431.67	20.87	412.07	28.00
			Cosine	408.90	20.89	328.66	30.33
Anisotropic Scaling	x⊙r	×rx ×ry	L1	258.74	33.91	459.69	39.71
			L2	550.67	18.48	1150.81	18.89
			Cosine	470.64	14.41	987.91	15.36
Homotheties	$r₀+r₁(x-r₀)$	×r₁	L1	400.44	23.67	627.74	27.63
			L2	501.25	21.17	750.74	31.90
			Cosine	403.52	26.89	938.44	36.51
Anisotropic homotheties	$r₀+r₁⊙(x-r₀)$	x y r₁x r₁y	L1	268.54	32.53	472.43	39.48
			L2	457.00	21.51	760.54	30.35
			Cosine	434.15	19.89	752.71	24.93
Element-wise affine	$r₀⊙x+r₁$	None	L1	262.95	33.21	420.30	40.09
			L2	417.50	22.87	692.14	32.32
			Cosine	401.14	21.20	738.38	26.19

Where ⊙ is the element-wise product and · the dot product.

FB15k is a subset of Freebase with 14951 entities, 1345 relations and 483142 training triplets.

When presented with a training triplet, the left and right score are computed for all 14951 entities, the scores are then sorted and we report as micro mean the mean rank of the correct entity and as micro top10 the percentage of correct entity placed in the top 10. The macro mean is the mean mean rank over all relation : the mean rank is computed for each relation and then the mean over all relation's mean rank is taken (the top10 is defined similarly).

Detailed visualisation of results.

Archive with (obsolete) results.

Combining models

The relations in the dataset are hard to analyse since we only have a subset of the graph defining it, however it seems natural that the optimal class of transformation depends on the relation. A first approach was implemented with a product of experts / mixture of models kind of model.

Results :

Models	Composition	FB15k
		Micro		Macro
		Mean	Top10	Mean	Top10
All L1	×	185.82	47.20	111.36	60.88

Still working on it. See [3].

Archive with (obsolete) results.

References

[1]: Mikolov, Tomas, et al. "Distributed representations of words and phrases and their compositionality." Advances in Neural Information Processing Systems. 2013.
[2]: Bordes, Antoine, et al. "Translating embeddings for modeling multi-relational data." Advances in Neural Information Processing Systems. 2013.
[3]: Hinton, Geoffrey E. "Training products of experts by minimizing contrastive divergence." Neural computation 14.8 (2002): 1771-1800.